Page 7

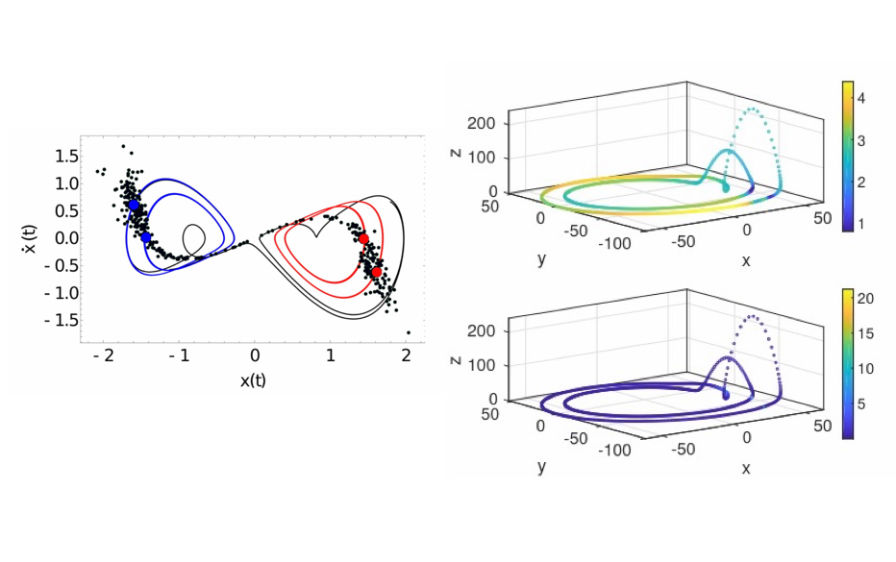
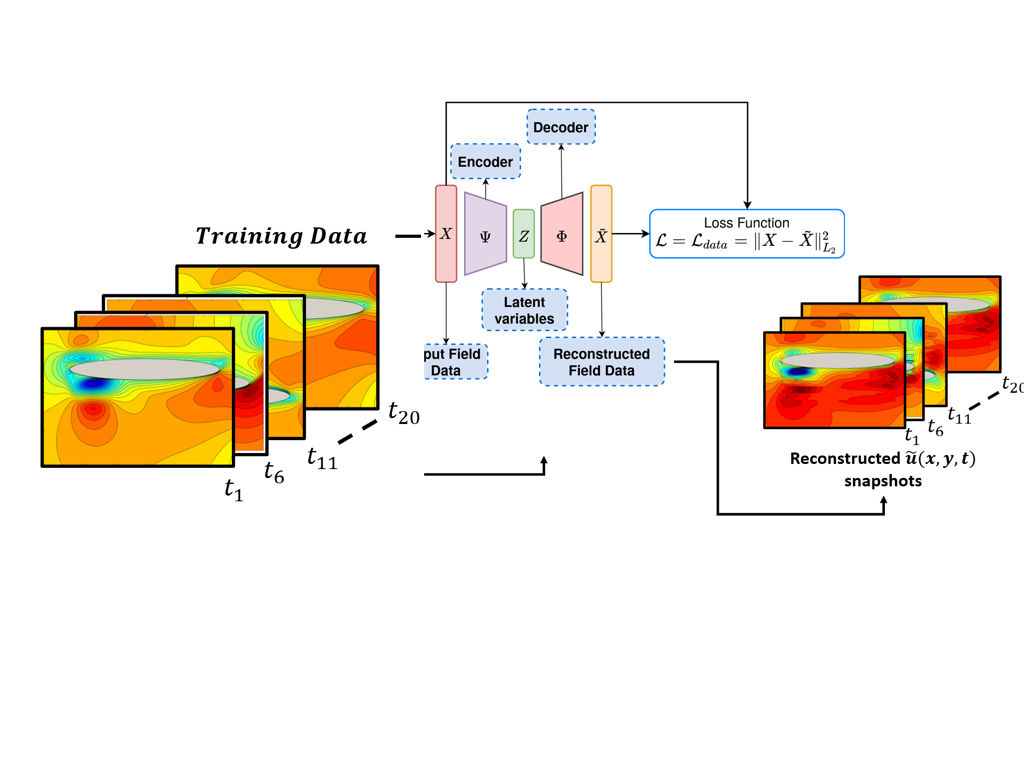
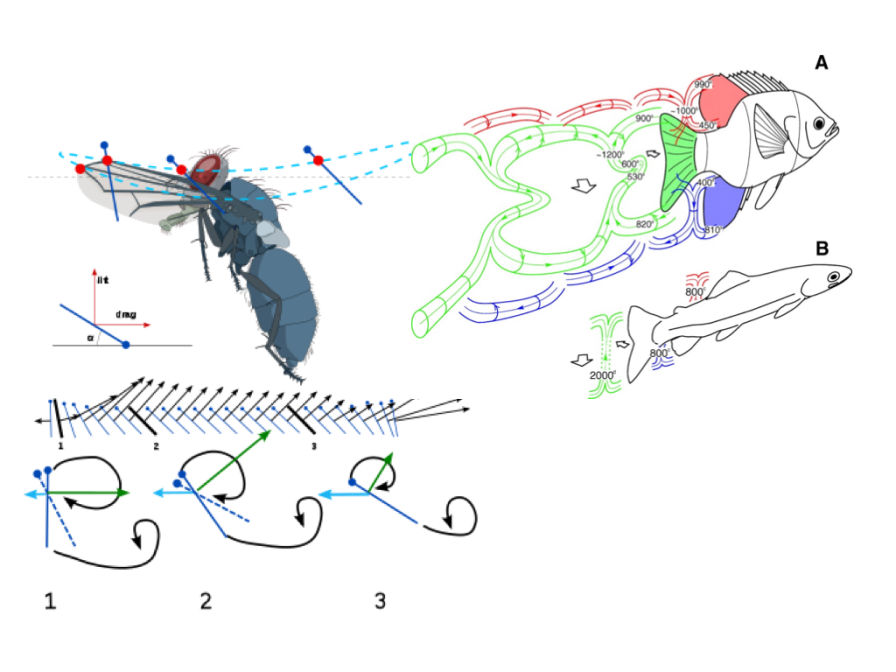
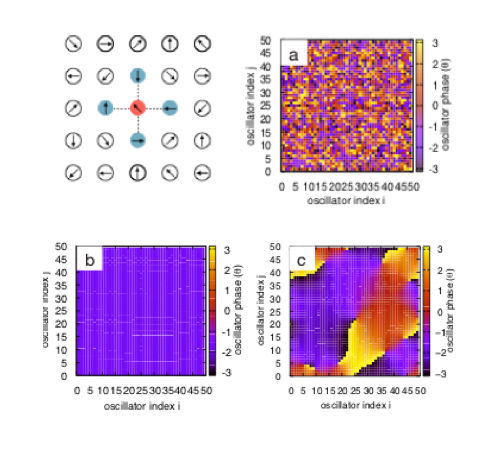
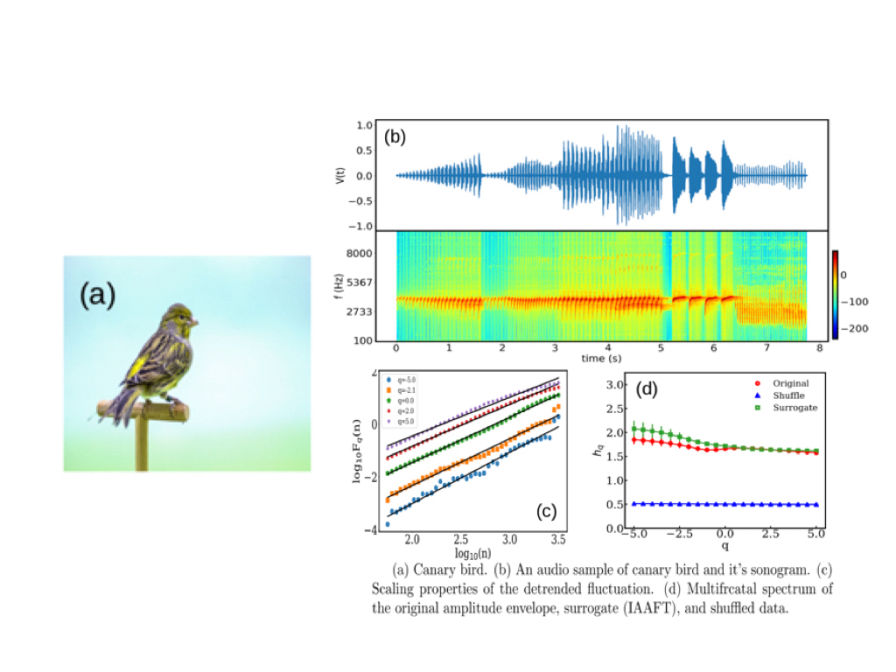
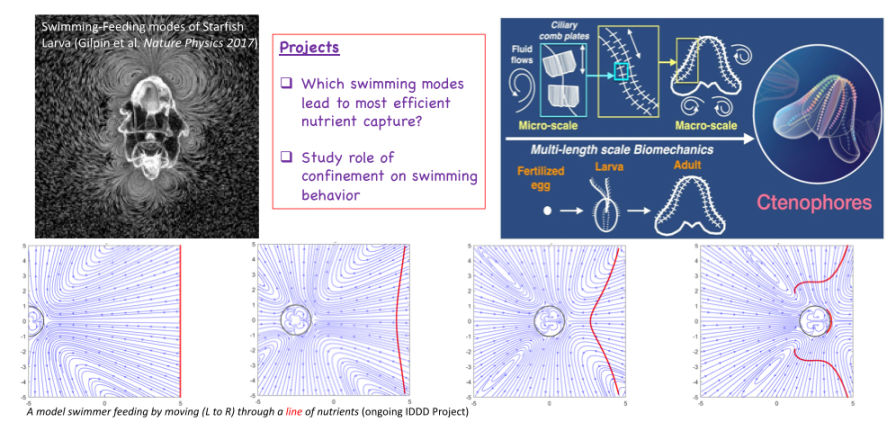
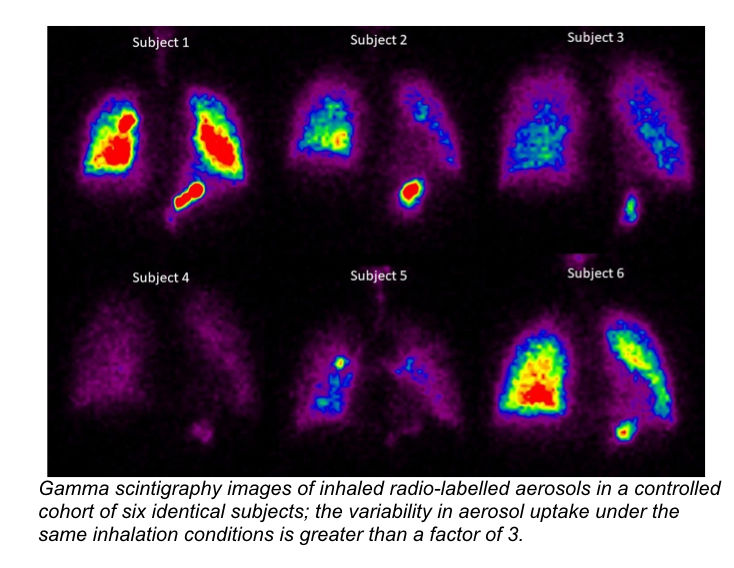
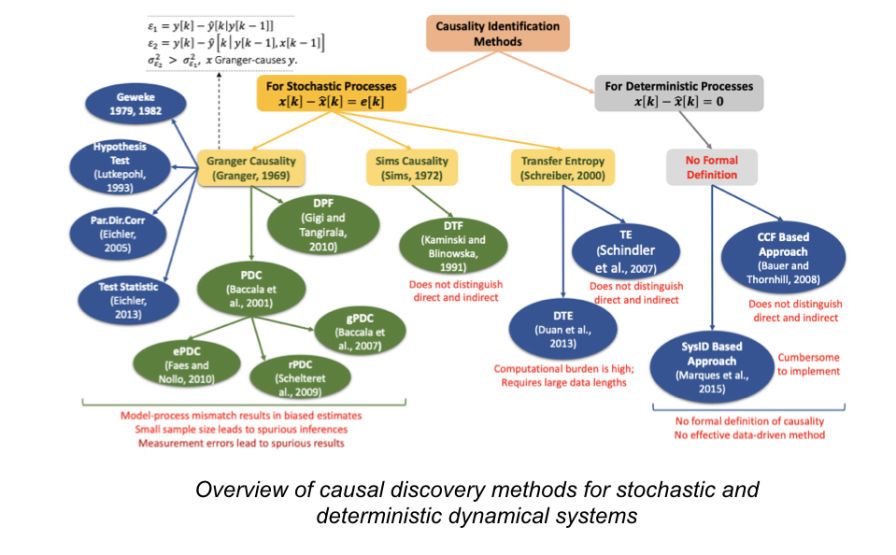
Mobirise

Q-Analysis of networks

A simplex in a network is clique of all-to-all connected nodes. Or, n-dimensional generalization of triangle.

A simplicial complex is a collection of simplices “glued” together along common faces.

The dimension of a simplicial complex is the dimension of the largest simplex in the structure, qmax.

Mobirise

Climate dynamics

El-Nino Southern oscillation (ENSO) is a phenomenon that disrupts weather patterns of the world. The warming phase is known as El Nino and the cooling phase is La Nina.

ENSO can be modelled as a complex network, where nodes are geographical locations and edges depend on the statistical similarities in climate records.

Before La Nina, the network's vertex tends to cluster.

Mobirise

Mobirise

Noise induced transitions

Noise plays a significant role in nonlinear dynamical systems. Noise can not only change the bifurcation behaviour but can lead to phenomena such as noise induced intermittency, basin hopping, stochastic resonance etc, all of which can have dramatic changes in the system behaviour.

These have important connotations in predictions of host of dynamical systems - from climate to engineering applications like aeroelastic flutter.

Mobirise

Machine learning: Complex flow fields

Fluid flow problems involve complex nonlinear interactions, multiple spatio-temporal scales, heterogeneous data.

Experiments, simulations are slow, expensive, so parametric analysis difficult.

Strong parametric dependence and important qualitative changes: need more database for parametric interpolation and extrapolation,

Strong motivation for the development of more effective ML techniques: hybrid techniques to combine ML wth first principles of physics?

Mobirise

Mobirise

Bio-mimetic flows

Interactions of key vortices and how they strengthen and weaken each other dictates the dynamics

ML provides new avenues for dimensionality reduction, data driven modelling, system identification

Existing data can help a latent space representation to evolve the spatio-temporal dynamics

Accurate and efficient reduction is size by capturing key flow-features/dominant patterns

Mobirise

Phase synchronization

Computational neuroscience models employ single neural models of three broad classes–rate code based, spike-based and oscillator-based. There are indeed neural models of oscillators that do not have the universality of both rate coded and spiking neuron network models. Oscillatory neuron models are used to model extensively oscillatory phenomena of the brain, like building generative models of cortical oscillations to understand brain rhythms and neuronal synchronization.

We aim to develop general, trainable oscillatory neural network models that can be used to simulate dynamic brain responses. The models might involve oscillator models like Kuramoto oscillator, Hopf oscillator, van der Pol oscillator, or other neural oscillator models like FitzHugh Nagumo, Morris- Lecar or Wilson-Cowan oscillators.

Mobirise

Bird song

The study of the characteristics of the birdsong, and the identification of a system which can produce a synthetic birdsong of the same characteristics, provides important insights in the ways in which the neural architecture in the brain can coordinate with a delicate vocal apparatus that the bird can and must control with high precision.

The tools required for this analysis draw from multidisciplinary areas neuroscience, dynamical systems, time series analysis, and recently, machine learning techniques and optogenetics. We hope to analyse the elements of bird song as well as the changes which occur in the structure of the birdsong in the development of the bird using tools such as Hurst exponents, simplicial characterisers, multifractals and complexity measures

Mobirise

Physics of living matter

Self-driven units, living or nonliving, capable of converting stored or ambient free energy into sustained states of motion comprise what is commonly known as active matter. These are non-equilibrium systems and are known to exhibit a high degree of collective behaviour due to their mutual interactions. Even in an isolated state, an active particle is a fascinating case study in dynamical systems.

In the proposed study we will investigate ciliary propulsion across different length scales using a combination of experimental, theoretical and simulation approaches.

Mobirise

DYnamics of human breathing

A dynamical network model of the breathing lung is being developed to simulate the flow of air through the lung during inhalation and exhalation. A parasitic model for aerosol deposition will be coupled. Finally, this coupled model will require parameters that are lung-specific. Such parameters will be extracted from desktop phantom bronchiole experiments where aerosol deposition will be measured using spectrometric techniques. Once the model is developed and populated with human lung relevant parameters, it will be exercised to test out a hypothesis related to the pathways that disease causing germs take to reach the bloodstream.

Mobirise

Reconstruction of causal dynamical networks of industrial processes

Modern industrial processes are complex with tighter integration of energy and material recycles. The complexity renders these processes obscure to a first-principles approach and therefore inaccessible to traditional mathematical models. Moreover, each application demands a different layer of information that is best modelled by a graphical or network approach.

The objective of this approach is to develop data-driven causal network or graphical model representations for industrial processes. These models are useful in determining disturbance propagation pathways, performance assessment/monitoring, fault diagnosis and alarm management.

Complex Systems & Dynamics Indian Institute of Technology Madras Chennai 600036 India